Бывает, что школьная математика, как зубная боль: справиться с ней самому невозможно. Ребенок со слезами решает домашку, родители с трудом пытаются помочь. В итоге, дроби, котангенс и теоремы превращается в ночной кошмар для семьи.
Что делать в этой ситуации? Предложить ребенку сочинить собственные математические задачи, затем самому найти их решение. И это не шутка, не розыгрыш, а серьезный совет от педагогов Маткласса. Они утверждают, что детей, неспособных к математике не существует. И доказывают это на собственной педагогической практике, в которой активно используют наглядные задачи.
Итак, если у ребенка не складываются отношения с цифрами, ему стоит начать с картинок и познакомиться с задачами, которым «не учат в школе». Какие же можно назвать наглядными?
В первую очередь те, условия которых нарисованы. Вместо текста — чертеж или рисунок, в котором содержится задание. К этому прилагаются краткие устные пояснения о том, что хотелось бы найти. Наглядные задачи особенно популярны в начальной школе, хотя нередко они находят отклик и у подростков. Задачи на симметрию, изометрию, аксонометрию также относятся к типу наглядных.
Наглядные задачи помогают включить дополнительные функции мозга через сравнения и воображение. И таким образом пробудить в ребенке жажду фантазерства и сочинительства.
Вот как складывается формула наглядной задачи:
+ увидел условия + появилась идея решения + воплотил идею в жизнь = получил результат
А классический пример такой задачи может выглядеть так:
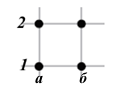
На листке в клеточку рисуются 4 точки, каждая из которых через буквенно-числовые символы имеет свою координату. Детям, с учетом возраста можно озвучить, что такое «координаты»: например, что имя точки, повторяет имя ребенка.
Рисуем «треугольник» и озвучиваем координаты (имена) вершин треугольника, рисуем все возможные варианты треугольников. На 4-х точках можно построить всего 4 (четыре) треугольника: 1а.2б.1б; 1а.2а.1б; 2б.2а.1б; 1а.2а.2б. Потом убираем чертеж и пробуем рисовать треугольники «по памяти», называя вслух координаты.
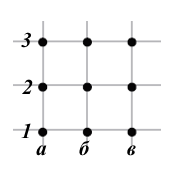
Более сложный вариант такого вида задач получается, если строить чертеж уже на поле с точками становиться 3х3 и количество вариантов возрастает, если говорить о треугольниках. Но на этом же поле (3х3) можно рисовать уже 4-х и 5-ти угольники. Чем больше углов, тем выше уровень сложности задачи.
Поле с точками можно расширить до 16 (4х4) и условия усложнить.
Пример:
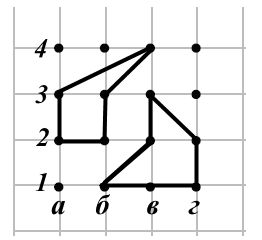
Еще один вид наглядных задач — задачи на разрезание. Допустим, даны такие фигуры. И их надо разделить на равные части:
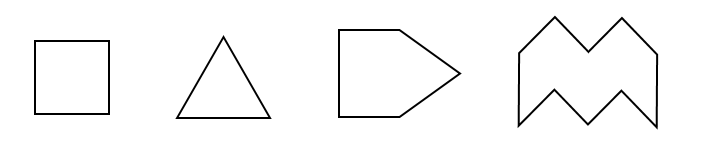
Или такие:

Или разделить на 3 (три) равные части:
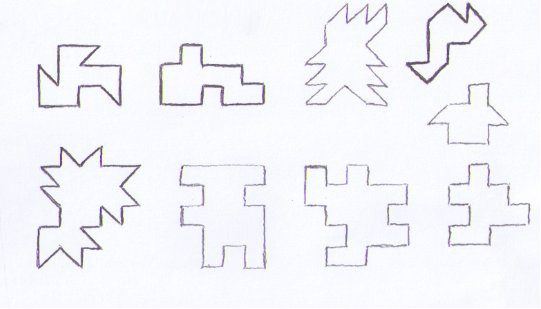
или на 4 (четыре) равные части:
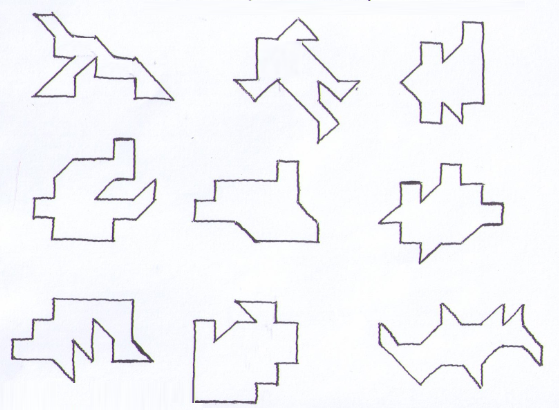
Типов наглядных задач существует десятки, формируются они по принципу: от простого к сложному.
Выполняя подобные задания, ребёнок шаг за шагом «тренируют мышцу» своего воображения, прокачивает критическое мышление, формирует новые нейронные связи.
Так он готовит себя ко встрече с более сложной математикой в виде текстовых задач. А еще учится мыслить нестандартно, думать как математик и фантазировать как поэт.
Записывайте своего ребенка на пробное бесплатное онлайн-занятие и познакомьте его с наглядными задачами!









