Не только решать, но и сочинять! (Часть 1)

Школьная математика представляется каждому как решение задач и примеров. А что, если посмотреть на математику с другой стороны и попробовать самим сочинить какую-нибудь задачу? И предложить решить её своим друзьям, одноклассникам, родителям, учителю.

Сочинять задачи не только невероятно интересно, но и очень полезно! Почему интересно? Да потому, что, сочиняя:

- ты чувствуешь себя экспертом! 

- ты понимаешь, что сочинять могут не только люди, которые составляют учебники или олимпиады, но и простые школьники!

Почему сочинять полезно? Потому что, когда ты сочиняешь:

- ты глубже разбираешься в определённом типе задач; это значит, что тебе будет легче учиться! 

- ты можешь сочинять задачи такой сложности, которая подходит именно для тебя!

Попробуем разобраться в вопросе, с чего начать сочинение задачи. Что важно и на что необходимо обратить особое внимание.

Наиболее интересны для решения и сочинения олимпиадные задачи. Так как они нестандартны и требуют особого подхода к решению. А вот сочинять их гораздо проще, чем может показаться на первый взгляд. 

Рассмотрим несколько типов задач из олимпиад прошлых лет и попробуем сочинить похожие задачи.

РЕШАЕМ

Задача 1. Разрежьте фигуру (по границам клеток) на три равные (одинаковые по форме и величине) части. Олимпиада 6-го класса по математике за 2012 год.

Решение.

Решить такую задачу не очень просто, а придумать – очень даже легко!

Начнём!

СОЧИНЯЕМ

Шаг 1.

Нарисуй фигуру из 4-6 клеток, например: 

Шаг 2.

Теперь «склей» несколько таких фигур:

Шаг 3. Перерисуй контур фигуры и напиши условие задачи. 

«Разрежьте фигуру (по границам клеток) на три равные (одинаковые по форме и величине) части».

РЕШАЕМ

Задача 2. Вася может получить число 100, используя десять троек, скобки и знаки арифметических действий: 100=(33:3−3:3)⋅(33:3−3:3). Улучшите его результат: используйте меньшее число троек и получите число 100.  

Олимпиада 6-го класса по математике за 2013 год.

Решение.

Ответ может быть таким: 100=333:3−33:3. Опять решение задачи заключается в переборе вариантов. 

Давайте теперь придумаем похожую задачу!

СОЧИНЯЕМ

Шаг 1. 

Придумай верный пример с умножением, делением, сложением, вычитанием, скобками, например:

12 * 3 + 45 – 6 + 7 + 8 = 90

Шаг 2.

Перепиши пример, убрав все знаки и скобки:

1 2 3 4 5 6 7 8 = 90

Шаг 3.

Запиши задание:

«Поставь арифметические знаки и скобки в выражение 1 2 3 4 5 6 7 8 = 90, чтобы оно стало верным».

Теперь приведём пример задачи 4-го класса. Почему 4-го? Не 6-го и не 7-го? Потому что такие задачи решаются довольно легко, если знаешь метод, а вот придумывать их не так-то просто, и если начать придумывать подобную задачу для 6-го класса, то можно быстро запутаться. 

РЕШАЕМ

Задача 3. Спортсмены A, B, C, D и E участвовали в забеге. Спортсмен D прибежал позже A, а спортсмен B раньше D и сразу за C. Спортсмен C не был первым, но прибежал раньше A. В каком порядке финишировали участники? Олимпиада 4-го класса по математике за 2019 год.

Решение.

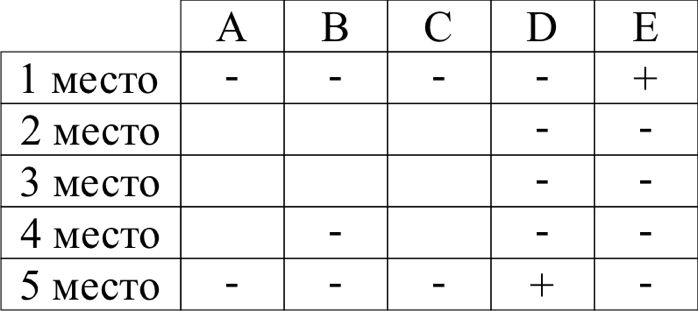
Для решения нарисуем таблицу:

В неё мы будем ставить + и – в зависимости от того занял ли спортсмен определённое место. Если D прибежал позже А, то D не занял 1 место, а спортсмен А не занял последнее место.

Так как В прибежал раньше D, но сразу за С, то D не занял и 2 место, а В не занял 5 и 1 места. С не был пятым и четвёртым (за ним как минимум В и D).

Спортсмен С не был первым, но прибежал раньше А: А не первый.

Первое место мог занять только спортсмен Е, ставим +

Исходя из того, что никакое другое место Е занять не мог, последнее место занял D.

Перечитаем условие ещё раз. Поскольку В прибежал сразу после С, он не мог быть вторым, а значит он третий, а спортсмен С – второй.

Проставляя знаки «-» в строках и столбцах, где уже есть «+», получаем, что А занял 4 место. 

На этом сегодня все! Вторая часть статьи с созданием подобных задач и решением других выйдет совсем скоро. Ссылка на нее появится здесь: Часть 2

Статью подготовлена для родителей и детей! Автор: Андрей, сын Юлии Кручининой, педагога олимпиадной математики, автора онлайн-курса «Геометрические подвиги в стране Олимпии» и организатора каникулярных программ в Зеленоградске