Единица может быть равна двойке?

Математики без причины не становятся. Кого-то тянет к числам, кому-то нравится строить математические системы, а кто-то занимается ей из-за другой специальности — программированию, инженерии или архитектуры. Существует более нетривиальная, но вполне частая причина увлечься математикой. Мы даже считаем её романтичной — когда любознательный ребенок, ломающий вещи, чтобы узнать, как они работают, задается вопросом: «Да почему это два плюс два это четыре, а не пять», и  что-нибудь подобное. 

Может посложнее, может попроще, но такой вопрос способен юного бунтаря, никогда не интересующегося науками внезапно заставить воспринимать любую математическую задачу как задачу, которую хочется решить. а не просто препятствие на уроке или при решении домашнего задания.

Понять, как работает математика. Не только дети, но и взрослые иногда находят причины увлечься математикой, потому что что-то их внезапно зацепило. Вот как, например, может зацепить такое (спойлер!) ложное утверждение:

2=1

Глупо? Да. но интересно, как к этому можно прийти.

Путь A=B. Начнем с такого утверждения, будем его раскрывать через простейшие алгебраические вычисления. 

ШАГ 1. A2 = AB

ШАГ 2. A2 + A2 = A2 +АB

ШАГ 3. 2A2= A2 +АB

Вы там не устали еще? :)

ШАГ 4. 2A2-2АB=A2+АB-2АB

ШАГ 5. 2A2-2АB=A2-АB

ШАГ 6.  2(A2-АB)=1(A2-АB)

ШАГ 7. Сокращаем! И что у нас получается??? 2=1

Итак, разбор по шагам: 

С этого момента мы будем использовать символ a для обозначения того же числа, что и b .

Может показаться, что использовать два разных символа ( a и b ) для обозначения одного и того же числа, неправильно. Но нет, в этом нет никакой проблемы. Буквы, используемые в алгебре, не имеют заранее определенного значения; это просто сокращения, которые можно использовать для обозначения всего, к чему хочется вернуться и к чему снова нужно будет обратиться.

ШАГ 1. Это следует из  a = b путем умножения обеих частей на a .

Если два числа равны, и вы умножите их оба на одно и то же число, результаты также будут равны.

ШАГ 2. Это следует из предыдущего шага (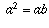) путем добавления 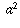к обеим сторонам.

Если два числа равны, и вы добавляете одно и то же число к обоим, суммы также будут равны.

ШАГ 3. Это следует из предыдущего шага (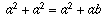) с применением упрощения .

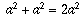ШАГ 4. Это следует из предыдущего шага ( 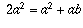) путем вычитания 2 ab из обеих частей.

ШАГ 5. Это следует из предыдущего шага путем вычленения 2 из левой части и вынесения 1 из правой части.
Закон распределения гласит, что x ( y + z ) = xy + xz для всех чисел x , y и z , и факторизация формула из прошлого шага - это просто применение этого к частному случаю x = 2, 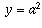 , и z = - ab.

Запись является допустимой, поскольку при умножении любого числа на 1 число остается неизменным.

ШАГ 6. Здесь также все по правилам.

И вот мы подходим к восьмому шагу. До этого никаких проблем не возникало. Все было по правилам математики. А что теперь?

ШАГ 7. Сокращая две части примера мы как бы делим их на одно и то же выражение. 

Однако деление имеет смысл только тогда, когда число, на которое вы делите, не равно нулю. В этом доказательстве, 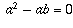поскольку на шаге 1 мы предположили, что a = b !

Следовательно, незаконно делить обе части уравнения на 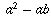, потому что это было бы деление на ноль, что не имеет никакого смысла (как объясняется ниже).

По сути, это доказательство сводится к утверждению: «1 умножить на 0 равно 2 умножить на 0, следовательно, 1 равно 2». Ошибка заключается в том, что тот факт, что два числа дают один и тот же ответ (ноль) после того, как вы умножаете их каждое на ноль, не обязательно означает, что эти два числа одинаковы, потому что все , что при умножении на ноль, дает ноль.

Это также причина того, что деление на ноль не имеет смысла: не существует только одного однозначно определенного числа q, такого 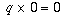, что нет никакого числа, которое мы могли бы однозначно и однозначно определить как частное 0/0.

Если вы попытаетесь разделить 1 (или какое-то другое ненулевое число) на 0, вы столкнетесь с другой проблемой: в этом случае нет такого числа q , что 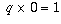, поэтому мы не можем определить частное 1/0.

Вот почему деление на ноль не определено (не только потому, что это правило кто-то придумал!)

Математика способна удивлять! И хорошо, что кто-то придумывает такие странные и заведомо ложные утверждения. Они вызывают интерес к науке, помогают найти ошибки в других задачах и попросту развлечься!

Такой должна быть математика: интересной, веселой и глубокой. А ваш ребенок хотел бы такой заниматься? У него есть возможность заниматься в онлайне или на очных кружка с одним из двадцати учителей, каждый — со своим подходом!

Узнайте больше о наших онлайн-кружках и летних лагерях